A sokasági eloszlásra, paramétereire vonatkozó feltevéseket statisztikai hipotéziseknek nevezzük.
A feltevés vonatkozhat:
- véges sokaság jellemzőire (átlag, arány, szórás)
- a sokasági eloszlás típusaira (normális, exponenciális stb.)
- a sokasági eloszlás paramétereire (várható érték, szórás stb.)
- a sokaságban érvényesülő összefüggéseket leíró modellek paramétereire.
A hipotézisek lehetnek egyszerűek és összetettek. Egyszerű, ha egy bizonyos értékkel való egyezést vizsgálunk:
Összetett, ha egyenlőtlenséget vizsgálunk. Pl.:
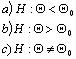
A hipotézisvizsgálat eszköze a statisztikai próba, mely egyoldalú alternatív hipotézis esetén egyoldalú próba, kétoldalú hipotézis esetén pedig kétoldalú próba.
A mintaelemek egy adott függvényként való felírását próbafüggvénynek nevezzük, melynek eloszlása a nullhipotézis helyessége esetén meghatározható.
A hipotézisvizsgálat végén el kell döntenünk, hogy a nullhipotézist elfogadjuk-e vagy nem.
A hipotézisvizsgálat során kétféle hibát követhetünk el:
- Elsőfajú hibát (I. hiba), ha elvetjük a nullhipotézist, holott a valóságban igaz.
- Másodfajú hibát (II. hiba), ha elfogadjuk a nullhipotézist, holott az hamis.
A hibát és elkövetési valószínűségük leolvasható az alábbi táblázatból:

Az elsőfajú hiba elkövetésének valószínűsége megegyezik a szignifikancia-szinttel. Ennek komplementere a próba megbízhatósági szintje. A másodfajú hiba valószínűségének komplementere pedig a próba ereje.
A két hiba valószínűsége csak egymás rovására csökkenthető.
A másodfajú hiba és komplementerének értékét nehéz meghatározni, pontosan akkor mondható meg nagysága, ha tudjuk mi az igaz, ha a nullhipotézis nem teljesül.
A másodfajú hiba valószínűségét felírhatjuk, ha bevezetjük értéket, melyre igaz, hogy
